본문
지수분포와 망각성질, 그리고 문제풀이
실제 과정을 확률과정으로 간략화 시킬때 많이 쓰는 방법으로 지수분포가 있다. 이는 실제 세계의 현상을 잘반영하기 때문이기도 하지만, 무엇보다 확률과정을 분석하기가 쉽기 때문이다.
지수분포의 가장 중요한 특성은 시간에 따라 영향받지 않는 예측이 가능하다는 것이다. 예를 들자면, 어떤 전구의 수명이 지수분포를 가진다고 하자. 한장소에 들어온 사람이 전구가 켜져 있는 것을 보았지만 그 전구가 언제부터 켜져있었는지 모르고 있다면, 그 전구는 앞으로 얼마나 더 켜져 있을 것이라고 생각할 수 있을까? 지수 분포에서는 이 전구의 남은 수명은 한번도 사용하지 않은 전구의 수명과 같은것으로 예측된다. 곧, 과거에 일어난 일이 미래의 일에 영향을 미치지 않는다는 것이다. 이 보기의 결론이 다소 이상하게 느껴지겠지만, 이렇게 느껴지는 이유는, 우리가 평소에 경험한 전구의 수명이 실제로 지수분포가 아닐때가 많이 때문이다. 하지만 실제 문제에는 지수분포로 간략화될 수 있는 모형이 많이 있고, 이런 이유로 지수 분포에서는 여러 응용분야에서 쓰인다.
* 지수분포(Exponential distribution) : Exp(λ)
* 망각 성질(memoryless property, forgetfulness)
지수분포의 중요한 성질로서, 망각 성질(memoryless property, forgetfulness) 가 있다. 아래 그림에서, s이후의 그래프는 전체의 그래프와 동일하다는 것이 특징이다. 따라서, { X>s }에서의 X의 분포 또한 지수분포를 갖는다. 예를 들어, 수명 X가 Exp(λ)를 따르는 전구를 생각해볼 수 있다. 전구가 s시간 동안 끊어지지 않을 확률은 P(X>s)로 나타낼 수 있다. 이제, s동안 끊어지지 않았다는 조건하에, 이후 t시간동안 끊어지지 않을 확률을 P(Y>t|X>s)로서 구해볼 수 있다.
 |  |
위의 결과에 의하면 s시간 동안 끊어지지 않았다는 조건 하에 앞으로 t시간 동안 끊어지지 않을 확률은 s에 무관하다. 즉, 얼마동안 켜져있었는가를 망각한다. 지수분포의 이러한 성질을 망각성질(memoryless property)이라고 부른다. 지수분포는 망각성질을 갖는 유일한 연속분포이다.
Pr(X>s+t|X>s) = Pr(X>t)가 구체적으로 의미하는 바는 전구의 수명이 지수분포를 따르면, "끊어지지 않고 켜있는 전구는 어느 시점에서 보거나 새 전구와 같다"는 것이다. 예를 들면 1시간 동안 끊어지지 않은 전구나 1000시간 동안 끊어지지 않은 전구나, 전구의 수명이 지수분포를 따르는 한 모두 동일한 새 전구와 같다.
* 지수분포의 또다른 성질
한 지수 랜덤 변수가 다른 하나보다 작은지 판별에 아래와 같이 계산해볼 수있다. 즉, X1과 X2가 독립 지수 랜덤 변수이고 각각 1/λ1, 1/λ2를 평균으로 갖는다고 했을때, P{X1<X2}는 얼마인가에 대해 생각해 볼 수 있으며, X1에 대하여 다음과 같이 풀이할 수 있다. 또한, X1, X2, ... Xn이 각각 μi의 비를 갖는 독립 지수 랜덤 변수라고 했을 때, Xi에서 가장 작은 값을 갖는 때는 μi의 총합만큼의 비를 갖는 경우이다. 또한, min(X1, ... Xn)의 CDF는 (λ1+ ... + λn)의 지수 분포를 갖는다고 할 수 있다. 이때 Xi가 가장 작은 값을 가질 확률은 아래 세번째 식에서 확인할 수 있다.
 |  |  |
문제 #20 (Chapter 5. The Exponential Distribution and the Poisson Process - Introduction to Probability Models에서)
서버 1과 서버 2를 통해(고객이 처음 도착했을때 서버1에서 서비스를 받고, 이후 서버2를 이용하며, 이 둘에게로부터 서비스를 받은 후에 떠나는), 사용자에게 서비스를 제공하는 시스템을 생각해보자. 서버 i에서의 서비스 시간은 μ1, μ2를 갖는 지수 랜덤 변수이다. 당신이 도착했을 때 서버 1은 이용 가능하였고, 서버2에는 두명의 사용자가 존재(A는 서비스를 이용하고 있고 B는 대기하고 있다)하고 있다고 할때 다음을 구해보자:
1) 서버 2로 옮겨갈 때 A가 아직 서비스를 받고 있을 확률인 P(A)
2) 서버 2로 옮겨갈 때 B가 아직 존재하는 확률인 P(B)
3) T가 시스템에 머무르는 시간이라고 할 때 E[T]
힌트) T=S1+S2+WA+WB 로 적어볼 수 있다. 여기서 Si는 서버 i에서 당신이 서비스 받는 시간, WA는 A가 서비스를 받는 도중 서비스 큐에서 대기하고 있는 시간, WB는 B가 서비스를 받는 도중 서비스 큐에서 대기하고 있는 시간을 나타낸다.
풀이)
1) A에게의 서비스가 끝나기 전에 서버 1에서 당신의 서비스가 완료되어 서버2로 넘어가려하는 경우, A는 아직도 서버2에서 서비스를 받고있는 상태일 것이다. 서버 2에 당신이 도착했을 때 A는 계속 서비스를 받고 있을 것이고, 지수 랜덤변수의 망각 성질에 의해, A가 받아야 할 서비스는 Exp(μ2)만큼이 남아있을 것이다. 또한 당신은 서버 1에서 Exp(μ1)의 서비스를 받는다. 따라서, P(A)는 Exp(μ1) 랜덤 변수가 Exp(μ2) 랜덤변수보다 작은 확률을 나타낸다 할 수 있을것이고 이를 P(A)=μ1/(μ1+μ2)으로 나타낼 수 있다.
2) (A에게 남은 서비스의 시간 + B에게의 서비스 시간) 보다 당신의 서비스 시간이 적게 된다면, 당신이 서버 2로 넘어가더라도 B가 아직 존재할 것이다. 우선, A가 당신보다 먼저 끝나는 경우와 당신이 A보다 일찍 끝나는 경우를 생각하고 그 후 B가 시스템에 머물러 있는 확률을 계산할 수 있다.
여기서, P(B in system|you finish before A) = 1 라고 할 수 있는데, 이것은 당신이 A에게 서비스가 종료되기 전에 서버 2로 옮겨 간 경우리므로 당연히 B는 시스템에 존재하기 때문이다. 만면에, 만약 A가 당신보다 서비스를 먼저 종료한다면, 여기에서도 역시 망각 성질로 인해, 당신이 서버 1에서 받아야 할 남은 서비스는 Exp(μ1)이고, B는 서버 1에서의 당신의 남은 서비스가 서버 2에서 B가 받아야할 서비스보다 적은 경우에 B는 계속 그곳에 있을 것이다. 따라서
3) 시스템에 당신이 머무를 예상시간을 계산하기 위해, 우선 T=T1+R로 나누는데, 이때 T1은 처음 사건이 발생할때까지의 시간을 의미하고, R은 그 외의 시간을 나타낸다. 처음 사건이 발생할때까지의 시간은 Exp(μ1+μ2)이고 따라서 E[T1]=1/μ1+μ2이다.
E[R]을 계산하기 위해, 서버2에서 A가 먼저 서비스를 끝마쳤는지 또는 서버 1에서 당신의 서비스가 먼저 종료되었는지에 대해 결정해야(condition on) 한다. 만약 서버 1에서 서비스가 먼저 종료된 경우(μ1/(μ1+μ2)), 서버 2로 옮겨갔을때, 당신의 시스템에서 남아있는 시간은, 서버 2에서의 A가 남아있는 시간과 서버 2에서의 B가 서비스 받는 시간, 그리고 서버 2에서 당신이 서비스 받는 시간으로 구성된다. A가 서버2에서 남아있는 시간은 역시 망각성질에 의해 Exp(μ2)이고, 따라서 당신이 남아있는 시간은 3/μ2가 될 것이다.
이제, 만약 서버 2에서 A가 먼저 끝나는 경우를 생각해 보자면, 당신이 시스템에 남아있게 될 기대시간은, 다음 사건(당신이나 B가 서비스를 마치게 되는)이 발생할때까지의 시간 + 사건 발생이후에 걸리게 되는 시간으로 계산할 수 있다. 후자를 계산하기 위해, 우리는 어떤것이 먼저 일어날것인가에 대해 결정해야 한다.
이 모든 과정들을 더함으로서 E[T]를 구할 수 있다.
참고문헌 : 확률모형 문제와 풀이, Introduction to Probability Models





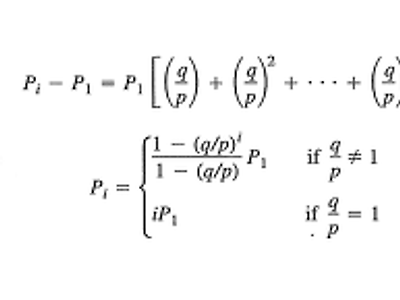
댓글