본문
ARE WE SPIRITUAL MACHINES? | Chapter 1 - #3. The Law of Accelerating Returns
무어의 법칙은 어떤것으로부터 유래하는 것일까? 이렇게 명확하게 예측할수있는 현상 뒤에는 어떤것이 있는것인가? 이러한 경향(trend)의 궁극적 근본에 대한 연구는 자주 다루어지지 않는다. IBM의 기초과학 원구원장인 Randy Issac이 말한대로, 단지 '업계의 기대와 목표치'에 불과한 것인가?
나의 관점에서 보자면, 이것은 기술의 진화과정(evolutionary process)이 지수적으로 성장함을 표현하는 방법중 하나이다. 진화과정이 가속화될 수록, 이에 따른 보상/결과/산출(returns, 예를 들어 성과 혹은 제품)은 지수적으로 증가한다. 계산능력의 지수적 성장은, 진화과정중에 지수적으로 성장하는 산출을 보여주는 매우 적절한 예시이다. 또한, 계산능력의 지수적 성장은 점차적으로 가속되고 있다. 1천달러 대비 MIP(Multiple in Power)을 달성하기 위해 처음에는 90년이 걸렸지만, 이제는 그정도의 수치가 매일같이 증가하고 있다.
무어의 법칙은 고정된 크기의 집적회로에 얼마나 많은 트랜지스터를 배치할 수 있는가라는 문제로 간단하게 나타낼 수 있으며, 또한 트랜지스터의 크기를 나타내는데 사용되기도 한다. 하지만, 크기나 숫자에 중점을 두기 보다, 더욱 이 속성을 잘 드러낼 수 있는 단위로, 단위원가당 계산속도(computational speed per unit cost)로 표현하는것이 더욱 좋을것이라 생각한다. 이 과정에서는 혁신, 즉 기술의 진화와 같은 '영리함(cleverness)'의 다양한 정도가 고려될 것이다. 집적회로에서의 혁신 뿐 아니라 컴퓨터 설계에 있어서 다양한 계층의 혁신이 존재하며, 여기에는 파이프라이닝(pipelining), 병렬처리, 예견 명령처리(instruction look-ahead), 명령어셋, 메모리 캐시등과 같은 것들을 생각해볼 수 있다.
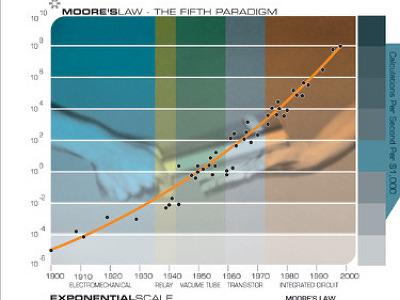
위 그림에서 보면, 계산능력의 지수적 성장은 집적회로의 시기(1958년대) 혹은 트랜지스터(1947년대)의 시기에서부터 이루어졌다고 하기 보다, 1890년과 1900년 사이에 미 통계청에서 사용된 '전기기계 계산기(electromechanical calculator)'의 시대에서부터 시작했다는것을 알 수 있다. 이 그림에서는 전자기계 계산기, 릴레이 기반 컴퓨터, 진공관 컴퓨터, 이산 트랜지스터 기반 컴퓨터, 그리고 마이크로프로세서에 이르는 컴퓨터의 서로 다른 5개의 패러다임을 동시에 보여주며, 여기에서 가장 마지막 부분에서만 무어의 법칙이 성립된다.
무어의 법칙이 2019년을 기점으로 더이상 효력을 발휘하지 않게될때(이때쯤이면 트랜지스터의 크기는 단지 몇개의 원자크기에 불과할것이기 떄문에), 이와 동시에 발생하게될 제 6의 패러다임이 무엇이 될것인가는 명확하다. 비록 단면의 회로를 제작하기 위해 20여개의 물질층이 필요하긴 하지만, 오늘날의 칩들은 단면으로 이루어져있다. 하지만 우리의 두뇌는 3차원으로 이루어져있다. 우리는 3차원의 세계에 살고있는데, 이를 활용하는건 어떨까? 회로를 3차원으로 구성할 수 있도록 해주는 다양한 기술들이 존재한다. 예를 들어 나노튜브는 이미 실험단계를 거쳤으며, 이를 통해 탄소 원자의 5각 배열으로 회로를 만들수 있다. 1세제곱인치의 나노튜브 회로는 인간의 두뇌보다 백만배 더욱 강력한 성능을 가지게 될 것이다.
따라서, 계산능력의 (이중)지수적 성장은 무어의 법칙에서 벗어난다. 또한, 계산능력의 가속화되는 성장은 곧, 위에서 설명한(진화과정의 가속화) 더 광범위한 현상의 일부를 보여주는 것이다. 다른 저서에서, 나는 과정의 '속도'와, 과정의 질서와 대비되는 '혼돈의 정도' 이 둘간의 상관관계에 대해 논의하였다. 예를 들어, 우주론적인 역사에서 본다면, 우주는 작은 혼돈으로부터 시작하였고 이때 처음, 3개의 주요한 패러다임이 아주 짧은 시간동안 생겨났다.(중력, 질량, 그리고 자연계에 존재하는 4가지의 힘). 이제는 방대한 혼돈의 환경에서, 우주적인 패러다임의 변화에는 매우 긴 시간이 필요할 것이다.
관찰자들은 트렌드라는 것이 자원에 종속적이라는 사실을 들어, 지수적 성장에 대한 예측을 비판한다. 이것의 가장 고전적인 예로, 생명체가 새로운 서식지를 찾았을때, 시간이 흐름에 따라 개체의 수가 증가하지만 식량이나 공간과 같은 '자원'이 동이나게 되면, 더이상 그러한 증가추세를 보이지 못한다는 것이다. 하지만 진화과정에서의 지수적 성장에 필요한 자원은 비교적 한계가 없다고 할 수 있다. 여기에서의 자원의 예를 들자면, 1) 진화적 과정 이 자체의 질서와 2) 진화적 과정이 이루어지는 환경에서의 (다양성을 부여해 주기도 하는)혼돈이 있다.
우리는 또한 S 곡선과 연속적(continuing) 지수적 성장 이 둘을 구분할 필요가 있다. S 곡선은 처음에는 너무나 느리게 발전하여 알아채기도 힘들지만 어느순간 급속도로 발전하고, 이후 성장이 둔화되며 점근선에 도달하는 형태를 취하며, '기술의 패러다임'을 대표하는 특성이다. 하지만 연속적 지수적 성장은 '기술의 진화과정'을 대표하는 특성이다. 집적회로에 더욱 작은 트랜지스터를 올려놓음으로서 더 빠르고 집중된 계산을 가능하게 하는, '무어의 법칙'과 같은 특정 패러다임은, 지수적 성장이 더이상 적용되지 않는 정도에까지 다다른다(즉, 성장이 둔화되며 점근선에 도달한다). 따라서 무어의 법칙은 S 곡선을 띈다. 하지만 계산능력의 발전은 연속적 지수형태를 보인다. S 곡선을 연속적 지수형태로서 변화시키는 것은 패러다임의 변화(즉, 혁신)이다. 이는 3차원 회로와 같은 새로운 패러다임이, 한계에 다다르게되는 오래된 패러다임에 이어 갈때를 의미한다. 계산능력의 역사에서 보자면 이미 이러한 과정은 적어도 4번 이루어졌다. 이러한 차이는 또한 인간외의 종들이 도구를 만들어 내는 과정과, 인간이 만들어낸 기술들을 구분해준다. 전자에서의 도구를 만들거나 사용하는 능력이 S 곡선으로 표현된다면, 후자에서는 성장에 있어 지수적인 형태를 띄고 이는 시초에서부터 계속 성장하는 모습을 보인다. 이에 관하여는 저서의 처음 2장동안 더 자세히 다룬다.
아래에, 계산능력의 지수적 성장과 관계가 있는, 수확가속의 법칙의 수학적 모델을 첨부한다. 아래의 공식들은 계산능력의 지속적인 성장을 나타내는 그래프를 설명한다. 이 그래프는 20세기에서의 데이터들을 잘 표현해주며, 또한 21세기에 대한 예측 또한 가능하게 해준다. 성장률 자체는 느리게 증가하지만, 지수적으로 표현된다는 것을 기억하자.
21세기에 적용될 또다른 기술적 트렌드로서 소형화(miniaturization)를 들 수 있다. 다양한 분야의 기술에서 구현의 크기 또한 이중 지수적 비율(double exponential rate)로 감소하고 있다. 현재는, 10년마다 약 5.6의 배율로 길이(크기)가 감소하고 있다.
===================
evolutionary process : 진화과정
(continuing) exponential growth : (연속적) 지수적 성장
computing (power) : 계산능력
출처 : http://taketimes.wordpress.com/category/the-singularity-is-near/
요즘 번역을 안하고 있다가 오랜만에 하려고 하니 감이 떨어졌는지 바로바로 한글로 옮겨지지 않는다. 굳이 한글로 옮기려면 성가신 문장들이 있어 대충 읽고 소화하여 내 말로 새로 만든 부분도 어느정도 있다. (특히 accelerate의 해석이 왔다갔다 하는것을 볼 수 있다) 아무튼 이번 절의 내용은, kurzweil의 중심적 생각인 'The Law of Accelerating Returns' 특히, '기술의 발전은 진화적인 성격을 띄며 따라서 그래프로 나타내자면 연속적인 지수 형태를 보여준다'는 것이다. 이 책이 나온 이후에 작성된 The singularity is near(특이점이 온다) 책에, 위에있는 설명을 알기 쉽게 그림으로 표현해놓았기에 첨부해본다.


댓글