본문
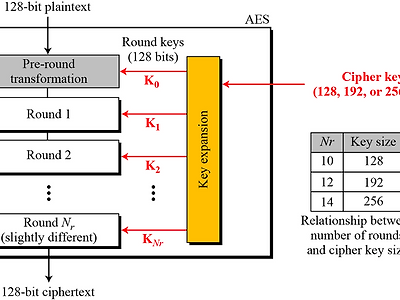
AES 문서 분석 #3. AES에서의 다항식 연산
이 글은 이전 포스팅(AES 문서 분석 #2. 다항식의 연산이론)과 동일한 이론을 기반으로 하는 AES 문서의 번역본입니다.
* 다항식의 합
유한체의 두 원소의 합은 다항식 내의 두원소에서의 동일한 승수를 가지는 항에서의 계수의 합을 통해 이루어진다. 이 합은 ⊕기호로 표기되는 XOR연산(즉, modulo 2)으로 이루어지는데, 여기서 1⊕1=0, 1⊕0=1, 0⊕0=0이 된다. 결과적으로, 다항식의 뺄셈은 다항식의 덧셈과 동일하다. 이러한 계산 과정 대신, 유한체 원소의 덧셈은 바이트에 해당하는 위치의 해당하는 비트에 대한 모듈로 2 덧셈으로 기술될 수 있다. {a7a6a5a4a3a2a1a0}과 {b7b6b5b4b3b2b1b0}의 각기 다른 두 바이트에 대해, 이 합은 {c7c6c5c4c3c2c1c0}으로 표현할 수 있으며 이때 ci=ai⊕bi(c7=a7⊕b7 .. c0=a0⊕b0) 이다. 따라서 아래와 같은 표기가 가능하다.
* 다항식의 곱
다항식 표현에서 GF(2^8)의 곱(•으로 표현한다)은 다항식의 곱에 8차 기약다항식(irreducible polynomial)을 모듈로 한것에 상응한다. 다항식은 나눌 수 있는 다항식이 자기 자신 하나만일 경우에 기약(irreducible)이라고 한다. AES 알고리즘에 있어, 사용되는 기약 다항식은 m(x)=x^8+x^4+x^3+x+1이며 16진수 표현으로 {01}{1b}이다.
m(x)을 통해 이루어지는 모듈라 감쇄(modular reduction)는 8차수 이하의 다항식으로 결과가 도출되도록 해준다. 덧셈과 달리, 바이트 레벨에서 이에 해당하는 더 간단한 연산은 존재하지 않는다. 곱은 associative하며(결합의((a x b) x c = a x (b x c)의 예에서처럼 계산식이 부분의 순서와 상관없이 동일한 결과가 나오는) 항등원은 {01}이다. 0이 아닌 8차 이하의 다항식 b(x)의 역원은 b^-1(x)이며, 확장 유클리드 알고리즘(extended Euclidean algorithm)을 사용하며 a(x)와 c(x)를 구하게 된다.
* x에 의한 곱
b(x)•x mod m(x)을 계산하여 최종 결과를 얻을 수 있다. 만약 b7=0이라면, 더이상 축약시킬 필요가 없다. 만약 b7=1이라면 m(x)을 사용하여 이를 축약할 수 있다. x({00000010} 또는 {02})를 곱하는 과정은 바이트 레벨에서 구현되며, 이는 left-shift와 뒤따르는 {1b}와의 선택적 XOR 비트연산으로 이루어진다. 바이트상의 연산으로 xtime()이 구현되며 이는 반복되어 사용될 수있다.
예를 들어 {57}•{13}={fe}는
* GF(2^8)에서의 계수가 존재하는 다항식
유한체 계수를 갖는 4개의 항이 있는 다항식 a(x)가 정의될 수 있다. 이는 [a0, a1, a2, a3]으로 표현되기도 한다. 참고로 이 절에 나오는 다항식은 기존의 유한체의 정의를 갖는 다항식과 약간 다르다. 이 절에 나오는 계수들 자체는 유한체의 원소이며, 비트 대신 바이트로 이루어져있다. 또한, 4개다항식의 곱은 아래에 나왔듯 다른 감쇄 다항식(reduction polynomial)을 사용한다. 이 구분에 대해 확실히 기억해 두어야 한다. 덧셈 연산과 곱셈 연산을 표현하기위해 두전째 4항다항식인 b(x)를 가정하자. 덧셈 연산은 각 워드에서의 해당하는 바이트들간의 XOR 연산과 동일하다.
곱셈은 두 단계를 거쳐 이루어진다. 첫번째 과정에서는, 다항식의 곱인 c(x)=a(x)•b(x)는 대수적으로 확장되고 제곱수에 맞춰 결합되어 아래와 같이 나타나진다.
결과로서 나오는 c(x)는 4바이트 워드를 나타내지 않기 때문에, 두번째 과정을 통해서 4차 다항식과 모듈로 연산을 진행함으로서 c(x)을 감쇄한다. 이를 통해 4차보다 낮은 차수를 가지는 다항식을 얻을 수 있다. AES 알고리즘에서는 x^4+1 을 사용하여 결과를 얻는다. (즉, x^i mod (x^4 + 1) = x^imod4) a(x)와 b(x)의 모듈라 곱인 a(x)⊗b(x)는 4항 다항식인 d(x)으로 아래와 같이 표현된다.
a(x)가 고정된 크기의 다항식일 때, d(x)는 다음과 같이 행렬 표현으로 작성될 수 있다. x^4+1이 GF(2^8)에서의 기약다항식이기 때문에, 고정 4항 다항식의 곱셈은 가역(invertible)일 필요는 없다. 하지만 AES 알고리즘은 가역인 고정 4항 다항식을 정의한다.
AES 알고리즘에서 사용되는 또다른 다항식은 a0=a1=a2={00}, a3={01}, 즉 x^3이다. 위 행렬은 입력 워드에서의 바이트를 회전하여 출력 워드를 생성하는 효과를 내기 위함이라는 것을 확인할 수 있다. 이것은 [b0, b1, b2, b3]이 [b1, b2, b3, b0]으로 변하는것을 의미한다.











댓글