본문
AES 문서 분석 #2. 다항식의 연산이론
* 다항식의 연산
다항식에 관한 연산은 두개의 연산을 포함하고 있다. 계수에 관한 연산과 두개의 다항식에 관한연산이다. 다시말해서, 두개의 체를 정의할 필요가 있다. 계수에 대한 체와 다항식들에 대한 체이다. 계수들은 0이나 1의 값을 가지므로 GF(2)체를 사용할 수 있으며, 다항식에 대해서는 GF(2^n)체가 필요하다.
다항식에 대한 연산을 정의하기 전에, 모듈로 다항식에 대해 살펴본다. 두 다항식의 덧셈은 결코 그 집합에 속하지 않는 다항식을 생성하지 않는다. 그러나 두 다항식의 곱셈은 n-1보다 큰 차수를 가지는 다항식을 생성할 수도 있다. 이것은 모듈로 논리에 따라, 곱셈한 결과를 모듈로 다항식으로 나누고 단지 나머지만 생각할 필요가 있음을 의미한다.(we need to divide the result by a modulus and keep only the remainder, as we did in modular arithmetic) GF(2^n)의 다항식들의 집합들에 대해서, 차수 n의 다항식의 군은 모듈로로써 정의된다. 이 경우에 모듈로는 소수 다항식(prime polynomial)로서 행동하는데, 그 집합에 있는 어떤 다항식도 이 (소수)다항식을 나눌 수 없음을 의미한다. 소수 다항식은 n보다 작은 차수를 가진 다항식으로 분해될 수 없다. 이러한 다항식을 기약다항식(irreducible polynomial)이라 한다. 각 차수에 대해서, 기약 다항식이 하나 이상 존재한다. 따라서 GF(2^n)을 정의할 때 모듈로로 사용할 기약 다항식을 반드시 정의해야 한다.
* 다항식의 덧셈
GF(2^8)에서의 계산은 아래와 같이 이루어질 수 있으며, ⊕는 다항식의 덧셈을 의미한다.
보다시피 덧셈에 대한 손쉬운 방법이 존재한다. 일치하지 않는 항은 그대로 쓰고 서로 일치하는 항은 삭제한다. GF(2)의 덧셈은 exclusive-or(XOR)연산을 의미하므로, 덧셈에 대한 결과를 얻기 위해 두 워드의 비트별로 exclusive-or연산을 할 수 있다.
다항식 자신을 더하는 더하는 것은 0의 다항식을 만들기 때문에 다항식의 덧셈에 대한 항등원은 0의 다항식이다(모든 계수가 0인 다항식) 그리고 GF(2)에서 계수를 가지는 다항식의 덧셈에 대한 역원은 바로 그 자신이다. 즉 뺄셈 연산은 덧셈 연산과 같음을 의미한다.
* 다항식의 곱셈
다항식의 곱셈은 첫번째 다항식의 각 항과 두번째 다항식의 각 항의 곱셈의 합이다. 곱셈에 대해서는 다음의 세가지 사실을 기억할 필요가 있다. 첫번째, 계수들의 곱셈은 GF(2)에서 이뤄진다. 두반째, x^i와 x^j를 곱한 결과는 x^(i+j)이다. 세번째, 곱셈은 n-1보다 큰 차수를 가지는 항을 생성할 수도 있다. 따라서 모듈로 다항식을 사용하여 곱셈한 결과를 줄일 필요가 있다. 먼저 위의 정의에 따라 어떻게 두 다항식을 곱하는지를 보인다.
최종 결과를 계산하기 위해서 차수 12의 다항식을 차수 8의 다항식으로 나누고(modulus) 나머지만을 취한다. 이 과정은 대수학에서의 나눗셈과 같다. 하지만 여기서 뺄셈은 덧셈과 같다. 곱셈에 대한 항등원은 항상 1이다. 예를 들면 GF(2^8)에서 곱셈에 대한 항등원은 00000001의 비트 형태이다. 그리고 곱셈에 대한 역원을 구하는 것은 더욱 복잡하다. 확장 유클리드 알고리즘이 반드시 모듈로와 다항식에 적용되어야 한다. 계산 과정은 정확히 정수에 대한 계산과 동일하다.
* 컴퓨터를 이용하는 곱셈
나눗셈 연산 때문에 두 다항식을 곱하기 위한 프로그램을 개발하는데 수반되는 효율성 문제가 있다. 컴퓨터의 구현에서는 줄여진 다항식에 x를 반복적으로 곱하는 더 나은 알고리즘을 사용한다. 예를 들어, (x^2⊗P2)을 계산하는 대신에 (x⊗(x⊗P2))을 계산하는 문제로 생각할 수 있다. 이 방법의 장점을 간략히 언급할 것이다. 하지만 우선 계산 과정을 보이기 위해 다음 예를 본다.
위의 알고리즘은 두가지 장점을 갖는다. 첫째, x에 의한 다항식의 곱셈은 n-비트 워드를 한비트 이동하면서 쉽게 계산할 수 있다. 이동(shift)연산은 일반적인 프로그램 언어에서 제공되는 연산이다. 둘째, 단지 다항식의 최고 멱승이 n-1일때만 그 결과가 줄여질 필요가 있다. 이 경우에 축소 (reduction)는 XOR 연산에 의해 쉽게 된다. 따라서 각 부분적인 결과를 구하기 위해 간단한 알고리즘을 설계할 수 있다.
1. 만약 이전 결과의 최상위비트가 0이면 단지 이전 결과를 왼쪽으로 한비트 이동한다.
2. 만약 이전 결과의 최상위비트가 1이면 왼쪽으로 한비트 이동하고, 최상위 비트를 제외하고 모듈로 다항식과 XOR한다.
크기 8의 비트 형식을 이용하여 위 곱셈을 계산할 수 있다.
P1=000100110, P2=10011110, modulus=100011010(9개 비트들)이다. ⊕는 XOR 연산을 의미한다.
P1⊗P2=(00100111)⊕(01001110)⊕(01000110)=00101111
이 경우에는 두 다항식들을 곱하기 위해 단지 다섯개의 왼쪽 이동연산과 네개의 XOR 연산이 필요하다. 일반적으로 차수 n-1의 두 다항식을 곱하기 위해 최대 n-1의 왼쪽 이동연산과 2n개의 XOR 연산이 필요하다.
GF(2^n)에서 다항식들의 곱셈은 왼쪽 shift 연산과 exclusive-or 연산들을 사용하여 계산할 수 있다.






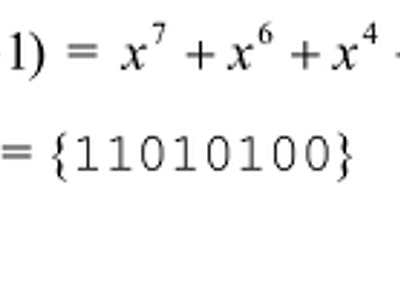

댓글